13 种高维向量检索算法全解析!
/ / 点击 / 阅读耗时 34 分钟编者按:
以图搜图、商品推荐、社交推荐等社会场景中潜藏了大量非结构化数据,这些数据被工程师们表达为具有隐式语义的高维向量。为了更好应对高维向量检索这一关键问题,杭州电子科技大学计算机专业硕士王梦召等人探索并实现了「效率和精度最优权衡的近邻图索引」,并在数据库顶会 VLDB 2021 上发表成果。
作为连接生产和科研的桥梁,Zilliz 研究团队一直与学界保持交流、洞察领域前沿。此次,王梦召来到 Z 星,从研究动机、算法分析、实验观测和优化讨论等维度展开讲讲最新的科研成果。
以下是他的干货分享,点击这里可获得论文全文
高维数据检索:基于近邻图的近似最近邻搜索算法实验综述
导言
向量检索是很多 AI 应用必不可少的基础模块。近年来,学术界和工业界提出了很多优秀的基于近邻图的ANNS 算法以及相关优化,以应对高维向量的检索问题。但是针对这些算法,目前缺乏统一的实验评估和比较分析。为了优化算法设计、进一步落地工业应用,我们完成了论文《A Comprehensive Survey and Experimental Comparison of Graph-Based Approximate Nearest Neighbor Search》。该论文聚焦实现了效率和精度最优权衡的近邻图索引,综述了 13 种具有代表性相关算法,实验在丰富的真实世界数据集上执行。我们的贡献可总结如下:
- 根据图索引的特征,我们将基于近邻图的 ANNS 算法划分为四类,这给理解现存算法提供了一个新的视角。在此基础上,我们阐述了算法间的继承和发展关系,从而梳理出算法的发展脉络;
- 我们分解所有算法为 7 个统一的细粒度组件,它们构成一个完整的算法执行流程,从而实现了算法的原子级分析。我们可以公平评估当前工作在某一组件的优化通过控制其它组件一致;
- 我们采用多样的数据集(包括 8 个真实世界数据集,它们包括视频、语音、文本和图像生成的高维向量)和指标评估当前算法的全面性能;
- 我们提供了不同场景下最优算法推荐、算法优化指导、算法改进示例、研究趋势和挑战的分析讨论。
研究动机
根据以下观测,我们对 13 种基于近邻图的 ANNS 算法进行了比较分析和实验综述:
- 目前,学术界和工业界提出 10 余种常见的近邻图算法,但对于这些算法的合理分类和比较分析较为缺乏。根据我们的研究,这些算法的索引结构可归结为 4 种基础的图结构,但这些图存在着非常多的问题,如复杂度太高等。所以,在这 4 种图结构基础上有多种优化,如对相对邻域图(RNG)优化就包含 HNSW、DPG、NGT、NSG、SPTAG 等算法。
- 很多现有的论文从“分子”角度评估基于近邻图的 ANNS 算法(宏观角度)。然而,我们发现,这些算法有一个统一的“化学表达式”,它们还可再向下细分为“原子”(微观角度),从“原子”角度分析可以产生一些新发现,比如很多算法都会用到某一“原子”(HNSW,NSG,KGraph,DPG的路由是相同的)。
- 除了搜索效率和精度的权衡之外,基于近邻图的 ANNS 算法的其它特征(包含在索引构建和搜索中)也间接影响了最终的搜索性能。在搜索性能逐渐达到瓶颈的情况下,我们对于索引构建效率、内存消耗等指标给予了重视。
- 一个算法的优越性并不是一成不变的,数据集的特征在其中起着至关重要的作用。比如,在 Msong(语音生成的向量数据集)上NSG 的加速是 HNSW 的 125 倍;然而,在 Crawl(文本生成的向量数据集)上 HNSW 的加速是 NSG 的 80 倍。我们在多样的数据集上执行实验评估,从而对算法形成更全面的认识。
近邻图算法“分子”级分析
在分析基于近邻图的 ANNS 算法之前,首先给大家介绍下 4 个经典的图结构,即:德劳内图(DG)、相对领域图(RNG)、K 近邻图(KNNG)、最小生成树(MST)。如图1所示,这四种图结构的差异主要体现在选边过程,简单总结如下:DG 确保任意 3 个顶点 x, y, z 形成的三角形 xyz 的外接圆内部及圆上不能有除了 x, y, z 之外的其它顶点;RNG 要确保(b)中月牙形区域内不能有其它点,这里的月牙形区域是分别以x和y为圆心,x 与 y 之间的距离为半径的两个圆的交集区域;KNNG 每个顶点连接 K 个最近的邻居;MST 在保证联通性的情况下所有边的长度(对应两个顶点的距离)之和最小。
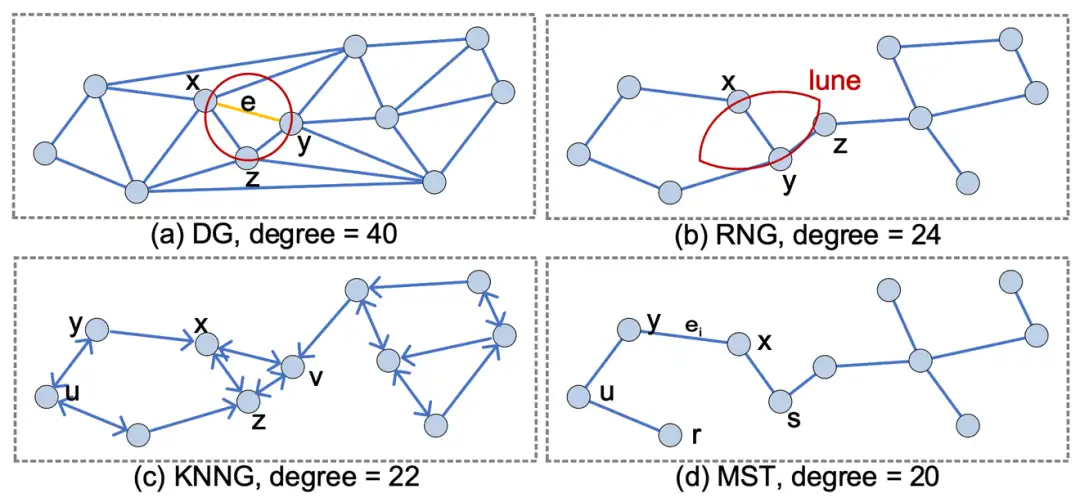
图1 四种图结构在相同的数据集上的构建结果
接下来,我将基于图1 中的 4 个图结构来梳理 13 个基于近邻图的ANNS算法。为了避免翻译造成了理解偏差,算法名使用英文简称,算法的原论文链接、部分高质量的中文介绍、部分代码请见参考资料。各算法之间更宏观的联系可参考论文中的表2 和图3。
算法1:NSW
NSW 是对 DG 的近似,而 DG 能确保从任意一个顶点出发通过贪婪路由获取精确的结果(即召回率为 1 )。NSW 是一个类似于“交通枢纽”的无向图,这会导致某些顶点的出度激增,从论文的表11 可知,NSW 在某些数据集上的最大出度可达几十万。NSW 通过增量插入式的构建,这确保了全局连通性,论文表4 中可知,NSW的连通分量数均为1。NSW 具有小世界导航性质:在构建早期,形成的边距离较远,像是一条“高速公路”,这将提升搜索的效率;在构建后期,形成的边距离较近,这将确保搜索的精度。
原文:https://www.sciencedirect.com/science/article/abs/pii/S0306437913001300
中文介绍:https://blog.csdn.net/u011233351/article/details/85116719
代码:https://github.com/kakao/n2
算法2:HNSW
HNSW 在 NSW 的基础上有两个优化:“层次化”和“选边策略”。层次化的实现较为直观:不同距离范围的边通过层次呈现,这样可以在搜索时形成类似于跳表结构,效率更高。选边策略的优化原理是:如果要给某个顶点连接 K 个邻居的话,NSW 选择 K 个距离最近的,而 HNSW 从大于 K 个最近的顶点里面选出更离散分布的邻居(见参考资料1)。因此,从选边策略考虑,HNSW 是对 DG 和 RNG 的近似。
原文:https://ieeexplore.ieee.org/abstract/document/8594636
中文介绍:https://blog.csdn.net/u011233351/article/details/85116719
代码:https://github.com/kakao/n2
算法3:FANNG
FANNG 的选边策略与 HNSW 是一样的,都是对RNG近似。FANNG 比 HNSW 更早提出,不过当前 HNSW 得到更普遍的应用,可能的原因是:(1)FANNG 的选边策略是在暴力构建的近邻图的基础上实现的,构建效率很低;(2)HNSW 通过增量式构建且引入分层策略,构建和搜索效率都很高;(3)HNSW 开源了代码,FANNG 则没有。
算法4:NGT
NGT 是雅虎日本开源的向量检索库,核心算法基于近邻图索引。NGT 在构建近邻图时类似于 NSW,也是对 DG 的近似,后续有一些度调整优化,其中最有效的路径优化也是对 RNG 的近似(论文的附件B 也给出了证明)。
原文1:https://link.springer.com/chapter/10.1007/978-3-319-46759-7_2
原文2:https://arxiv.org/abs/1810.07355
代码:https://github.com/yahoojapan/NGT
算法5:SPTAG
SPTAG 是微软发布的向量检索库,它的构建过程基于分治策略,即迭代地划分数据集,然后在每个子集上构建近邻图,接着归并子图,最后通过邻域传播策略进一步优化近邻图。上述过程旨在构建一个尽可能精确的 KNNG。在搜索时,SPTAG 采用树索引和图索引交替执行的方案,即先从树上获取距查询较近的点作为在图上搜索的起始点执行路由,当陷入局部最优时继续从树索引上获取入口点,重复上述操作直至满足终止条件。
原文1:https://dl.acm.org/doi/abs/10.1145/2393347.2393378
原文2:https://ieeexplore.ieee.org/abstract/document/6247790
原文3:https://ieeexplore.ieee.org/abstract/document/6549106
中文介绍1:https://blog.csdn.net/whenever5225/article/details/108013045
中文介绍2:https://cloud.tencent.com/developer/article/1429751
代码:https://github.com/microsoft/SPTAG
代码使用:https://blog.csdn.net/qq_40250862/article/details/95000703
算法6:KGraph
KGraph 是对 KNNG 的近似,是一种面向一般度量空间的近邻图构建方案。基于邻居的邻居更可能是邻居的思想,KGraph 能够快速构建一个高精度的 KNNG。后续的很多算法(比如 EFANNA、DPG、NSG、NSSG)都是在该算法的基础上的进一步优化。
原文:https://dl.acm.org/doi/abs/10.1145/1963405.1963487
中文介绍:https://blog.csdn.net/whenever5225/article/details/105598694
代码:https://github.com/aaalgo/kgraph
算法7:EFANNA
EFANNA 是基于 KGraph 的优化。两者的差别主要体现在近邻图的初始化:KGraph 是随机初始化一个近邻图,而 EFANNA 是通过 KD 树初始化一个更精确的近邻图。此外,在搜索时,EFANNA 通过 KD 树获取入口点,而 KGraph 随机获取入口点。
原文:https://arxiv.org/abs/1609.07228
中文介绍:https://blog.csdn.net/whenever5225/article/details/104527500
代码:https://github.com/ZJULearning/ssg
算法8:IEH
类比 EFANNA,IEH 暴力构建了一个精确的近邻图。在搜索时,它通过哈希表获取入口点。
原文:https://ieeexplore.ieee.org/abstract/document/6734715/
算法9:DPG
在 KGraph 的基础上,DPG 考虑顶点的邻居分布多样性,避免彼此之间非常接近的邻居重复与目标顶点连边,最大化邻居之间的夹角,论文的附件4 证明了 DPG 的选边策略也是对 RNG 的近似。此外,DPG 最终添加了反向边,是无向图,因此它的最大出度也是非常高的(见论文附件表11)。
原文:https://ieeexplore.ieee.org/abstract/document/8681160
中文介绍:https://blog.csdn.net/whenever5225/article/details/106176175
算法10:NSG
NSG 的设计思路与 DPG 几乎是一样的。在 KGraph 的基础上,NSG 通过 MRNG 的选边策略考虑邻居分布的均匀性。NSG 的论文中将 MRNG 的选边策略与 HNSW 的选边策略做了对比,例证了 MRNG 的优越性。论文中的附件1 证明了NSG的这种选边策略与 HNSW 选边策略的等价性。NSG 的入口点是固定的,是与全局质心最近的顶点。此外,NSG 通过 DFS 的方式强制从入口点至其它所有点都是可达的。
原文:http://www.vldb.org/pvldb/vol12/p461-fu.pdf
中文介绍:https://zhuanlan.zhihu.com/p/50143204
代码:https://github.com/ZJULearning/nsg
算法11:NSSG
NSSG 的设计思路与 NSG、DPG 几乎是一样的。在 KGraph 的基础上,NSSG 通过 SSG 选边策略考虑邻居分布的多样性。NSSG 认为,NSG 过度裁边了(见论文表4),相比之下 SSG 的裁边要松弛一些。NSG 与 NSSG 另一个重要的差异是,NSG 通过贪婪路由获取候选邻居,而 NSSG 通过邻居的一阶扩展获取候选邻居,因此,NSSG 的构建效率更高。
原文:https://ieeexplore.ieee.org/abstract/document/9383170
中文介绍:https://zhuanlan.zhihu.com/p/100716181
代码:https://github.com/ZJULearning/ssg
算法12:Vamana
简单来说,Vamana 是 KGraph、HNSW 和 NSG 三者的结合优化。在选边策略上,Vamana 在 HNSW (或 NSG)的基础上增加了一个调节参数,选边策略为 HNSW 的启发式选边,取不同的值执行了两遍选边。
原文:http://harsha-simhadri.org/pubs/DiskANN19.pdf
中文介绍:https://blog.csdn.net/whenever5225/article/details/106863674
算法13:HCNNG
HCNNG 是目前为止唯一一个以 MST 为基本构图策略的向量检索算法。类似SPTAG,HCNNG 的构建过程基于分治策略,在搜索时通过 KD 树获取入口点。
原文:https://www.sciencedirect.com/science/article/abs/pii/S0031320319302730
中文介绍:https://whenever5225.github.io/2019/08/17/HCNNG/
近邻图算法“原子”级分析
我们发现所有的基于近邻图的 ANNS 算法都遵循统一的处理流程框架,该流程里面有多个公共模块(如图2 的 C1->C7)。当一个近邻图算法按照该流程被解构后,我们可以很容易了解该算法是如何设计组装的,这将给后续近邻图向量检索算法的设计带来很大的便利性。此外,我们也可固定其它模块,保持其他模块完全相同,从而更公平地评估不同算法在某一模块实现上的性能差异。

图2 近邻图向量检索算法遵循的统一流程框架图
接下来,我们以 HNSW 和 NSG 为例,说明如何实现图2 的流程框架分析算法。在此之前,我们要先熟悉这两个算法的索引构建和搜索过程。首先是 HNSW 分解,HNSW 的构建策略是增量式的。因此,每插入一个数据点都要执行一遍 C1->C3 过程。
HNSW 分解流程:
| 模块 | HNSW 具体实现 |
|---|---|
| C1 | 生成新插入点所处的最大层;获取搜索入口点 |
| C2 | 新插入点作为查询点,从入口点开始,贪婪搜索,返回新插入点一定量最近邻作为邻居候选 |
| C3 | 启发式选边策略 |
| C4 | 无额外步骤,最高层中的顶点作为入口 |
| C5 | 无额外步骤,增量式构建已隐式确保连通性(启发式选边又一定程度破坏连通性) |
| C6 | 最高层的顶点作为入口 |
| C7 | 最佳优先搜索 |
NSG 分解流程:
| 模块 | NSG 具体实现 |
|---|---|
| C1 | NN-Descent 初始化近邻图 |
| C2 | 顶点作为查询,贪婪搜索获取邻居候选 |
| C3 | MRNG 选边策略 |
| C4 | 全局质心作为查询,贪婪搜索获取最近顶点作为入口 |
| C5 | 从入口开始,DFS 确保连通性 |
| C6 | C4 获取的入口 |
| C7 | 最佳优先搜索 |
由于 HNSW 的 C3 与 NSG 的 C3 是等价的,因此,从上面两个表格可知,HNSW 与 NSG 这两个算法差别并不大。其实,论文涉及到的 13 种算法中很多算法之间都是很相似的,详见论文第 4 章。
实验观测和讨论
具体的实验评估请参考论文第 5 章,接下来将概括介绍一下实验的观测结果和讨论:
不同场景下的算法推荐
NSG 和 NSSG 普遍有最小的索引构建时间和索引尺寸,因此,它们适用于有大量数据频繁更新的场景;如果我们想要快速构建一个精确的 KNNG(不仅用于向量检索),KGraph、EFANNA 和 DPG 更适合;DPG 和 HCNNG 有最小的平均搜索路径长度,因此,它们适合需要 I/O 的场景;对于 LID 值高的较难数据集,HNSW、NSG、HCNNG 比较适合;对于 LID 值低的简单数据集,DPG、NSG、HCNNG 和 NSSG 较为适合;NGT 有更小的候选集尺寸,因此适用于 GPU 加速(考虑到 GPU 的内存限制);当对内存消耗要求较高时,NSG 和 NSSG 适合,因为它们内存占用更小。
算法设计向导
一个实用的近邻图向量检索算法一般满足以下四个方面:
- 高构建效率
- 高路由效率
- 高搜索精度
- 低内存负载
针对第一方面,我们不要在提升近邻图索引质量(即一个顶点的邻居中真实的最近邻居所占的比例)上花费太多的时间。因为最好的图质量(可通过图中与距它最近的顶点有边相连的顶点所占比例度量)不一定实现最佳搜索性能(结合论文中表4 和图7、8)。针对第二方面,我们应当控制适当的平均出度,多样化邻居的分布,减少获取入口点的花费,优化路由策略,从而减少收敛到查询点的邻域所需的距离计算次数。针对第三方面,我们应当合理设计邻居的分布,确保连通性,从而提升对陷入局部最优的”抵抗力”。针对第四方面,我们应当优化邻居选择策略和路由策略,从而减小出度和候选集尺寸。
优化算法示例
基于上面的向导,我们组装了一个新的近邻图算法(图3 中的 OA),该算法在图2 中的 7 个组件中每个组件选中现存算法的一个具体实现,即 C1 采用 KGraph 算法的实现;C2 采用 NSSG 算法的实现;C3 采用 NSG 算法的实现;C4 采用 DPG 算法的实现;C5 采用 NSSG 算法的实现;C6 采用 DPG 算法的实现;C7 采用 HCNNG 和 NSW 算法的实现。OA 算法实现了当前最优的综合性能,详见论文原文。因此,我们甚至不用优化当前算法,仅仅把现存算法的不同部分组装起来就可以形成一个新算法。
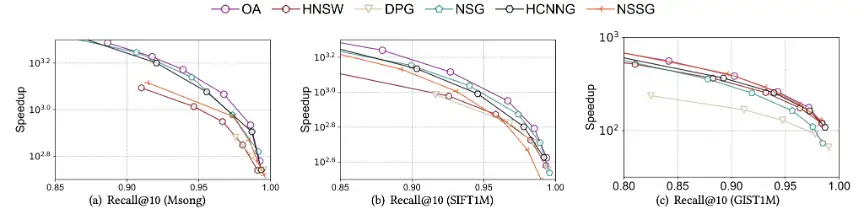
图3 OA 算法与当前最优的近邻图算法的搜索性能对比
趋势与挑战
基于 RNG 的选边策略设计在当前近邻图向量检索算法的效率提升中起到了关键作用。在论文的评估中,唯一一个基于 MST 的算法 HCNNG 也表现出来很好的综合性能。在上述纯近邻图算法基础上,后续发展有三个主要方向:
- 硬件优化;
- 机器学习优化;
- 更高级的查询需求,比如结构化和非结构化混合查询。
我们未来面对这三个挑战:
- 数据编码技术与图索引如何有机结合以解决近邻图向量检索算法高内存消耗问题;
- 硬件加速近邻图索引构建减少近邻图索引构建时间;
- 根据不同场景的特征自适应选择最优的近邻图算法。
参考资料
https://blog.csdn.net/whenever5225/article/details/106061653?spm=1001.2014.3001.5501
✏️ 关于作者:
王梦召,杭州电子科技大学计算机专业硕士。主要关注基于近邻图的向量相似性检索、多模态检索等研究内容,并在相关方向申请发明专利三项,在数据库顶会 VLDB 和 SCI 一区 top 期刊 KBS 等发表论文两篇。
日常爱好弹吉他、打乒乓球、跑步、看书,他的个人网站是 http://mzwang.top,Github主页是 http://github.com/whenever5225